筑波大学が2021年から導入した、学生の進学選択方法の改革事例を説明する。この研究テーマは、すでに実装がされており、センター長の栗野と研究員で横浜国立大学教授の熊野がかかわったものである。
大学が求める要件に合わせて、マーケットデザインの手法により、既存のマッチング理論を応用して実装を進めた手順を体感して貰えると幸甚である。
※本記事は、共立出版「マーケットデザイン総論」の7章にある「7.4 ケーススタディ:筑波大学の進学選択」と同様の記載内容です。前提知識についてより深い理解を得るには、同著を購入し、熟読されることやKumano and Kurino(2022)を参照されることをお勧めする。
Chap.1:事例の背景
Summary:筑波大学における学生の進学選択改革にマーケットデザインの手法を適用するに至った背景を説明する。既存の入試システムで発生している問題に対して、筑波大学が目指す結果を達成するための制度を設計するにあたり、既存のアルゴリズムでは目的を達成できないため、栗野、熊野に声がかかった。
筑波大学の入試システムの概要
まず、筑波大学の従来の入試制度について紹介する。通常の大学の学部や学科に相当するものを筑波大学では学群と学類と呼ぶ。1つの学群は、複数の学類によって構成されている。図1は、2020年時点での学群と学類の構成状況である。
それぞれの学群、学類には定員が定まっており、学類の定員の和が学群の定員と一致している。以前の入試システムでは、各学生が、1 つの学類に志願する仕組みであった。そのため、複数の学類への志願することはできず、ある学類に落ちた場合は、筑波大学に落ちたことと同等であった。すると、ある学生にとって「本来はある学類を第一志望とするにもかかわらず、落ちることを避けるためにより人気の低い学類へ志願する」という行動も散見された。それは、「本当にその学類で学びたい学生が入学できなくなること」も引き起こす。本来の希望と異なる学類へ進学した学生は、そこで新たに学問の楽しさを見出せればよいが、そうでない場合はやる気が続かなくなってしまうかもしれなく、ひいては、学業不良や留年、中退につながってしまう。つまり学生と学類のマッチングに問題が発生していた。(これは筑波大学に限った話ではなく、多くの大学、そして公立高校でも起こっている問題である。)
筑波大学の入試制度改革
既存の課題を解決するために、筑波大学は2016年より、2020年度からの入試制度の改革に取り組むことになった。大まかな改革方針は、入試の段階で特定の学群・学類を決定しない「総合学域群」として学生を受け入れる枠を設け、入学後に一定期間学んだ上で、本人の希望に応じて学類を選択できる仕組みを導入するものである。これは、東京大学は北海道大学ですでに取り入れられている進学選択と呼ばれる制度の導入である。ここで重要になるのは、入学後、どの学類へ学生を振り分けるかという問題である。学生の希望がいくつかの学類に集中してしまうと、定員の問題からどうしても学生の選抜が必要になるからである。
筑波大学に特有な条件は、既存アルゴリズムでは対応がかなわない
東京大学の進学選択では、近年、「先着順メカニズムのみ(ボストンメカニズム、または受入即決メカニズムとも呼ばれる)」から「先着順メカニズムとDAメカニズムの併用」に変更された。筑波大学でもDAメカニズムは1つの有力な候補として挙げていた。しかしながら、筑波大学の進学選択には他大学とは異なる要素が存在した。それは、学生の希望を最大限に汲み取るために、学群の定員は一定としながらも、その学群に配属される学類では定員の融通を可能にすることを改革の要素として含むことであった。この要素は非常に重要で、DAメカニズムをただ導入するだけでは問題が発生してしまう。その理由として、DAメカニズムが定員を固定した上でしか機能しないことが挙げられる。これでは、定員を融通できるせっかくの特色が全くいかされない。さらには、定員が変動することで、定員が固定された場合に得られたマッチングが、その中では望ましくても、定員の変動までを考慮すると正当な羨望が発生してしまうことが起こり得る。
マーケットデザインによるメカニズムの提案活動を開始
本センターの研究員である栗野と熊野は、この改革に対して、上記の問題を解決する新しいマッチングアルゴリズムを提唱した。そのメカニズムは実際に2021年(2020年入学の学生が進学選択を行うのは2021年であるため)から筑波大学において使用されている。以下では、マーケットデザインの思想に則って、著者らがどのようにして新しいメカニズムを提唱するに至ったかを紹介する。
Chap.2:【特定】定員調整可能なマッチング問題
Summary:【特定】章では、対象とする市場を重要な要素に限定して写像し、数学的なモデルとして特定します。筑波大学の進学選択制度は、生徒と学群・学類の非分割財マッチング市場ということはわかりますが、今回は、それに加えて「定員が可変」という要素が含まれるため、これを数学的に表現することが重要になります。
他大学の"進学選択"と異なる要求は?
Chap.1で述べた通り、筑波大学は改革の 1 つとして進学選択を行うことになった。進学選択は、学生と学類のマッチング問題である。そして、筑波大学からは以下を満たすようなマッチングメカニズムを構築したいとのことであった。
- 制約:学群の定員は一定としたまま、属する学類の定員をこれまでの定員をベースにある程度調整できるようにしたい。
これはとても興味深い提案であるとともに、既存のマッチング理論の枠を少しはみでていた。つまり、既存のマッチング問題とは異なる制約が追加的に課されたのである。制約と書くと、既存の状況よりも可能性が狭くなるように感じるが、以下の制約はむしろ可能性を広げている。そのため既存のマッチング理論を拡張する必要性がでてきた。
「定員を調整する」とは、簡単に言えば、学群内の学類間で幾許かの定員を融通し合うことである。ある学群に A と B の学類があり、それぞれの初期の定員が 10 名であったとしよう。もし A 学類を希望する学生が初期の定員よりも多い 12 人であり、B 学類には 8 人しか希望学生がいなかった場合、B 学類の定員を 8 名に減らし、その分浮いた定員 2 名を A 学類に追加して 12 名とすることを定員を調整するという。このとき、A、B 学類は同じ学群に属するので、学群の定員には変化はない。
このように特有の制約があるため、筑波大学のマッチング問題は、定員が固定になっている基礎的なマッチング環境で描写できない。そのため、定員調整を可能とするマッチング環境を新たに設定する必要がある。
今回の市場を数学的に記述すると?
ここまでで、市場を数学的に説明する条件をいったん整理する。通常の非分割財マッチングの市場に加えて、定員が変動することが制約として加わっていることが特長となっていることを念頭に置くと、下記のようなモデルとなる。
筑波大学での進学選択を市場として捉えたモデル
・\(N\):学生の集合(任意の学生を\(i\in N\)と書く)
・\(X\):学類の集合(任意の学類を\(x\in X\)と書く)
・\(K\):学群の集合(任意の学類を\(k\in K\)と書く)
学類\(x\)はただ1つの学群に属する。\(X_k\subset X\)を学群\(k\)に属する学類の集合とする。
・\(R_i\):学生の学類に対する選好
・\(q_x\):学類の定員( 変動可能 )
・\(\overline{q}_x\):学類の最大定員(固定)
・\(q_k\):学群の定員(固定)
ここでこれまでのモデルと異なる点は、学類の定員が変動する点である。学群\(k\) に属する学類の定員は \( \sum{x \in X_k} q_x = q_k\)を満たす。これより、変動可能な学類の定員の集合は
\[Q = \lbrace q \in \mathbb{Z}_+^{|X|} \mid \forall k \in K , \displaystyle \sum_{x \in X_k} q_x = q_k, かつ \forall x \in X , 0 <q_x < \overline{q_x} \rbrace \]
となる。このとき、\(Q\) の中のどの定員の組み合わせ\( q\) が学生にとって望ましい学類選択を与えるかは容易にはわからない。
Chap3:【確認】問題の所在の確認
Summary:【確認】章では、現状の市場が、制度上狙った結果を達成できているかを確認する。今回の市場は、まだ実際に運用が開始していない市場であるため、「定員を固定してDAアルゴリズムによる運用をした場合」を前提して、問題の所在を確認した。結果として、定員を調整できることによって、定員が固定されたDAアルゴリズムよりもより良い安定マッチングが存在する可能性が示唆されている。
各学類の定員が調整できるようになると、外生的に与えられた初期の定員の下での安定マッチングは実は学生の厚生を改善する余地があることがわかる。それは、最初に設定された定員とは異なる定員の下で得られる安定マッチングを学生全体が弱い意味で好むことがあるからである。
DAアルゴリズムよりも良い安定マッチングが存在する具体例(▶をクリックして展開)
4 人の学生 \(i_1, i_2, i_3, i_4\) と 3 つの学類 \(x, y, z\) があるとする。学類 \(x\) と\(y\) は学群\( k\) に属しており、\(z\) は\( k^′\) に属しているとする。それぞれの学類の定員上限は\( x \)と\( y\) が\( 2 \) 人、\(z\) が\( 1\) 人とし、学群の定員を \(k\) は\( 3\) 人、\(k^′\) は \(1\) 人とする。これより設定可能な定員の組み合わせは
\[Q = \{(1, 2, 1),(2, 1, 1)\}\]
となる。ここで \(Q\) の要素は定員ベクトルであり、左から \(x, y, z\) の定員 \(q_x,q_y, q_z \) を表す。各学類の学生に対する優先順位は以下とする。
\[ \begin{array}{ccccc}
≻_x \ : & i_1 & i_4 & i_2 & i_3 \\
≻_y \ : & i_3 & i_2 & i_4 & i_1 \\
≻_z \ : & i_2 & i_3 & i_1 & i_4
\end{array}\]
大学は、4 人の学生の選好を知る前に定員を設定しなければならない。そのため、大学が初期定員を \(q = (2, 1, 1) \) に設定したとする。そのとき、学生の選好が、
\[ \begin{array}{ccccc}
R_{i_1} \ : & y & x & ∅ & \ \\
R_{i_2} \ : & x & z & y & ∅ \\
R_{i_3} \ : & x & y & ∅ & \ \\
R_{i_4} \ : & y & x & z & ∅
\end{array}\]
であったとすると、\(q\) の下での学生最適安定マッチング \( \mu \) は
\[ \mu = \begin{pmatrix} i_1 & i_2 & i_3 & i_4 \\ x & z & y & x \end{pmatrix} \]
となる。\( {}^{*4}\) もし仮に定員を \( q^′ = (1, 2, 1)\) に設定していたとすると、そのときに得られる学生最適安定マッチング \( \mu^′\) は
\[ \mu^′ = \begin{pmatrix} i_1& i_2& i_3 & i_4 \\x & z & y & y \end{pmatrix} \]
となり、µ よりも全学生にとって弱い意味で好ましくなる。
一方で、大学が初期定員を \( q^′ = (1, 2, 1) \) に設定していたとしよう。そのとき、学生の選好が
\[ \begin{array}{ccccc}
R^′_{i_1} \ : & y & x & z & ∅ \\
R^′_{i_2} \ : & x & y & ∅ & \ \\
R^′_{i_3} \ : &x &y & z & ∅ \\
R^′_{i_4} \ : & y & z & ∅
\end{array}\]
であったとすると、\(q^′\) の下での学生最適安定マッチングよりも \(q\) の下での学生最適安定マッチングの方が全学生にとって弱い意味で好ましくなる。
ある定員の下で、学生の厚生を最も高める安定マッチングが達成されるとき、その定員を最適な定員と呼ぶ。具体例から示唆されることは、最適な定員は学生の希望(選好)に依存して変動することである。ここで重要なことは、学生の選好はマッチングを行う際に初めて明らかとなる。そのため、最適な定員を事前に設定することは不可能である。
定員が調整できるとき、定員をどのように設定するかは実は非常に難しい問題である。いわゆる初期の定員は外生的に与えられた定員である。一方で、学生の希望によって調整される定員は内生的に定まる。定員が調整できる上で、初期の定員を内生的に最適な定員に調整する、すなわち学生の厚生を最も高める安定マッチングに調整する仕組みこそが、栗野、熊野らが新しく考案するべきメカニズムである。
Chap.4:【目的】筑波大学の理想を定義式にする
制度設計者(筑波大学の学務)の「望ましさ」の整理
定員の調整が可能である場合、一般に初期の定員とは異なる定員の下で学生の厚生を高めることが可能であることがわかった。一方で、厚生以外にも進学選択マッチングに求められるものが存在する。そのため、このような新しいマッチング環境の下での「望ましいマッチング」を定めることから始めなければならない。カスタムメイドな制度設計では、制度の設計者である筑波大学が「何を望ましいと考えるか」が望ましさの指標となる。マーケットデザイナーは、言語的な要望をマッチング理論の枠組みで「翻訳する」必要がある。この橋渡しを間違えると、出来上がるメカニズムが全く設計者の意図せざるものとなってしまう。横着してこの作業をとばし、設計者の要望を自分の知識の範囲内で勝手に解釈してしまうことを避けるためにも、セカンドオピニオンは重要である。
筑波大学が進学選択制度に求める「望ましさ」の条件
- 定員調整可能な限りで、学生の希望する学類への進学をさせたい
- (既存の定員のために発生する)留年者を減らしたい
- 学生間に不公平が発生しないようにしたい
要望Aと要望Bは、前述したように定員調整による学生の厚生の改善である。そして「可能な限り」という点から、ただ厚生改善すればよいだけでなく、これ以上厚生改善の余地がないようなマッチングを達成したいということになる。これは効率性である。要望Cは、厚生とは異なる安定的なマッチングを達成したいということになる。よって、この 3 つの要望を同時に達成するマッチングが、今回の目的となる「望ましさ」である。既存の理論からもわかるように効率性と安定性は同時には成立しない。そのため、効率性と安定性のどちらに重きを置くかを相談した結果、安定性を重視することになった。以上を鑑みて、著者らが翻訳したマッチングに求める「望ましさ」は以下の事後的安定性という概念である。
【定義:事後的安定性】
マッチング \( \mu \) が事後的安定であるとは、\( \mu \) はある定員の組み合わせ \( q \in Q \)の下で安定的かつ、全ての \( q \in Q \) の下での安定的なマッチング \( \nu \) にパレートの意味で支配されないことをいう。
事後的安定マッチングは、学生の選好が事前にわからなくても、結果として学生の効率性が最大化される定員の組み合わせの下での学生最適安定マッチングである。つまり、制度設計者がうまく定員の設定を行えたならば、達成できるレベルで最も学生の効率性を高める安定マッチングに相当する。これは安定性の定義からもわかることであるが、最もよい定員を設定することは、留年者を最も減らすことと同等である。
望ましいマッチングは、あらゆる状況で存在するのか
結果に求める「望ましさ」は定まったが、そのような望ましいマッチングはいつでも存在しないと制度が成り立たない。この存在問題に対して、著者らは事後的安定マッチングがいつでも存在することを示した。
定理:定員調整可能なマッチング問題において、事後的安定マッチングは常に存在する。
事後的安定性以上に好ましいマッチング結果は存在しないのか
これより、著者らは次のステップである実践的なメカニズムの設計に進むことになる。しかし、事後的安定性は筑波大学の要望を最も反映したものなのか、という問いが発生する。先に述べたように、セカンドオピニオンは重要である。筑波大学においても、著者らの考え方を押し付けるのではなく、代替的な方法について議論を行った。Kamada and Kojima (2015) は同様の環境において目標定員を先に設定し、それに可能な限り近い安定マッチングの導出方法を発見している。よって、著者らは、関係者とともに、それぞれの解概念を筑波大学の要望に照らし合わせて吟味することにした。
Kamada and Kojima (2015) のメカニズムでは目標定員が先に設定されなければならない。これは、制度設計者が達成したい定員目標を強くもっている場合に相当する。実際、Kamada and Kojima (2015) の焦点は、研修医マッチング制度であり、研修医を僻地の病院にも可能な限り配分することが政策目標にあった。そのため、彼らは事前にある目標定員に最も近い安定マッチングを発見する方法を編み出した。これは目標定員にできる限り近い安定マッチングである一方、その犠牲として研修医の厚生が最大限には改善されない特徴がある。対して、筑波大学は、安定性を担保した上で、できる限り学生の希望に沿った進学選択を目的としている。そのため、今回は事後的安定性を望ましい結果として採用することとなった。
Chap.5:【方法】大学が求める制度は存在するのか
しかし既存のマッチング理論では解決できない重要な問題がある。それは、学生の選好は事前に知ることができないということである。事前に知ることのできないパラメータを所与として事後的安定マッチングは規定されるため、事後的安定マッチングは既存の理論では発見できない。
これに対して、最もシンプルな方法として、全ての q に対して DA アルゴリズムを 1 つ 1 つ計算し、その結果を見比べるという方法は存在する。しかし、Q は一般には指数的となるので計算量の問題に直面する。よって、このシンプルで原始的な方法は、実践不可能である。そのため Kumano and Kurino(2022) は 定員調整過程 (quota adjustment process ; QAP) と呼ばれる事後的安定マッチング(および対応する最適な定員)をとても短い時間(多項式時間)で発見するアルゴリズムを開発した。
QAPの外観
QAP はアルゴリズム内で定員数を最適に調整する。QAP のインプットは、学生の選好に加えて初期の定員である。アルゴリズム自体は本書のレベルを超えるので、割愛するが、興味のある読者は「現代経済学の潮流」または「マッチングの本」を参照されたい。5) 簡単な QAP の外観を説明すると、QAP は 2 つのステップで構成されている。QAP の主たるアルゴリズムは、このうち第 2 ステップにある。
・第1段階(初期定員による学生最適マッチングの導出)
QAP はまず最初に、初期の定員を用いて学生最適マッチング\( \mu_1 \)を求める。これは定員を初期の定員にした場合の DA の結果である。第 1 ステップは、定員を調整しながら学生の厚生を改善するためのいわばベンチマークとなる。
・第2段階(サイクル特定→再マッチングのループプロセス)
現状のマッチング結果\( \mu \)に対して、下記のプロセスを実施する。第2段階最初の\( \mu \)は、第1段階で得られたマッチング結果\( \mu_1 \)を使用する。
- 現状のマッチング結果\( \mu \)を参照して、より好ましい学類のある学生を、その学類と学生のベクトルとしてすべて書き下す。また最大定員まで到達していない任意の学類について、その学類とダミー学生というベクトルを学群に 1 つ用意する。そして、これらのベクトルを頂点として、特定のサイクルを見つけ出す。このサイクルは複数存在する場合があるが、そのときは任意のサイクルを 1 つ選ぶ。特定のサイクルが存在しなくなったところで、第2段階は終了とする。この時点での、マッチング結果 \( \nu \)と定員\( q_{\nu} \) が、QAPのアウトプットとなる。
- 選択したサイクルに従って、学類と学生のマッチング結果を調整する。ここで選択した特定のサイクルは、安定性を担保したまま定員とマッチングの更新を実施できるようにするための要素である。調整が完了したマッチング結果\( \mu^′ \)をインプットとして、再度第2段階をスタートする。
開発をしたQAPについて、栗野、熊野らは以下の重要な同値定理を明らかにした。
【事後的安定性の性質】
ある定員の下での安定マッチングが事後的安定マッチングである。\( \iff \)QAP第2段階における特定のサイクルが存在しない。
この同値により、事後安定マッチングを、QAPによって特定可能であることが説明できる。もしある定員の下での安定マッチングが事後的安定マッチングではなかったとすると、必ず特定のサイクルを見つけることができる。よって、特定のサイクルが見つかる限りは、事後的安定マッチングには到達していないことがわかる。もしこの方向が成り立たないと、事後的安定マッチングに到達できない。つまり定員調整によって安定性を担保したまま学生の厚生を改善する余地を残したままとなる。また事後的安定マッチングに到達した時点で特定のサイクルはなくなるので、事後的安定マッチングに到達したことがわかる。もしこの方向が成り立たないと、事後的安定マッチングに到達したにもかかわらず、特定のサイクルが見つかってしまい、安定性を失ったマッチングにさらに更新されてしまう。
QAP は上の定理に沿った定員とマッチングの更新を行うので、以下の系がえられる。
系:QAP は事後的安定マッチングを出力する。
事後的安定マッチングは、定員調整可能なマッチング問題に一般に複数存在する。そのため QAP はランダムにそのうちの1つを出力する。聡明な読者であればお気づきであろうが、QAP はその計算ステップにランダムな選択を許容する構造となっている。それが QAP が導出する事後的安定マッチングが一意とならない理由である。理論的には、異なる事後的安定マッチングは学生全体にとっては、厚生の優劣がつかないので、どちらも厚生の観点から「よい」マッチングには違いない。一方で、異なる事後的安定マッチング間では、片方を好む学生ともう一方を好む異なる学生が必ず存在する。筑波大学では、QAP のランダム選択の箇所でランダムには選ばず、いくつかの基準に従った選択方法を採用している。6)
望ましい結果が設定された後、制度設計者が懸念すべき事項は、そのアルゴリズムがうまく機能するか、すなわちインセンティブの制御ができているかである。DA などのようにインプットに対してアウトプットが一意的に定まる場合は、真実表明が支配戦略となる SP が重要なインセンティブ制御のための性質であった。QAP はインプットに対してアウトプットを1つ定めるが、一意的ではない。そのため、アルゴリズムのインセンティブ制御には、SP を拡張した「一般化された SP」を満たすかどうかが重要となる。(多価関数)メカニズムが一般化された SP を満たすとは、嘘の表明によって得られる結果の中に、真の表明で得られる全ての結果をパレートの意味で支配するような結果が存在しないことを指す。仮に、与えられた選好プロファイルから、すべての事後的安定マッチングを出力するようなメカニズム(これを"事後的安定マッチング対応"という)であれば、一般化されたSPを満たすことがわかっている。
定理:"事後的安定マッチング対応" は一般化された SP を満たす。
よって、 事後的安定マッチング対応はインセンティブ制御の面からもよい性質を保持している。(QAPについての議論は更新予定)
Chap.6:【調整】実装に向けて関係者への理解を促す
ここまでで、理論的には機能しそうなアルゴリズムが構築された。しかし、理論的に「よい」からといって、すぐに利用しようとするのは早計である。社会実装にはそれ相応のコストがかかる。また現実と理論の間には必ずギャップがある。そのため、十分な改善を見込めなければ、どんなに理論的に優れていても現実に使用するには及ばない。また多くの関係者を説得することができない。やってみないとわからないことも当然あるが、導入には極めて慎重にならなければならない。
そこで、著者らは QAP がどの程度優れているかをシミュレーションで定量的に評価することにした。一般的に受け入れられている先着順は、今回の目的からは大きく外れているので除外する。目的に最も近い既存の方法である DAを用いた場合と QAP を用いた場合の差を求めることにした。以下は 2 つのメカニズムの差である。DA で得られるマッチングを基準として、QAP によって何人の学生が DA よりも好ましい学類にマッチできたかを表している。注意しておくことは、QAP の下で DA よりも厚生が悪化する学生はいかなる場合にも存在しないことである。よって評価基準は、改善する学生が十分にいるかどうかである。
シミュレーションでは、学生の選好と学類の優先順位をランダムに 10,000回発生させた。そして同条件下で、DA と QAP(X) の差(の平均)を求めている。ここで QAP(X) の括弧内の X は、許容される定員の変動割合を指している。例えば、QAP(5) は(DA の計算に用いる)初期定員に対して各学類が 5%まで定員を変動させること(学群内の定員の和は一定の条件下で)ができることを意味する。また、3 種類の選好と優先順位の発生方法を試した。無相関は学生の学類に対する選好、学類の学生に対する優先順位をそれぞれ独立に発生させた場合を指す。相関がある場合については、学生間で学類に対する選好に正の相関をもち、また同一学群内の学類間で学生に対する優先順位に正の相関をもつように発生させた。相関が強ければ強いほど、同様の選好や優先順位をもつことになる。括弧内の強弱は、その相関度合いを指す。独立な場合に比べて、相関の導入はより現実的な状況を模倣しているといえるかもしれない。実際、人気のある(多くの学生が進学したい)学類があることや、同じ学群に属する学類では学生に求める条件が似通っていることが見受けられるからだ。
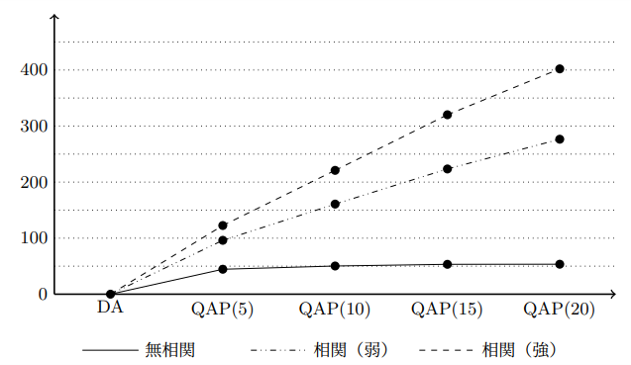
図:DAに対してQAPで構成改善した学生の(平均)数
シミュレーション結果 グラフからもわかるように、学類の定員を数パーセント上下させられるだけでも、多くの学生が改善していることがわかる。この理由は簡単で、ある学類の定員が増えたことで、ある学生がその学類に入れたとすると、その学生が移動前にいた学類で 1 つ枠が空く。そこにまた別の学生が入れることになり、この連鎖が発生する(連鎖の最後の学生が最初の学生と同じ学群であれば、学群の定員は一定に保たれている)。よって、たった 1 人分でも定員に変化あれば、それはマッチング全体に影響がおよび、改善の連鎖によって多くの学生が改善していくことになる。
これより、定性的にも定量的にも QAP が優れていることが示されたので、筑波大学では QAP の導入が決定した。著者らが筑波大学の関係者からもれ聞いた話では、DA を使っていた場合には留年することになっていたであろう学生が、QAP によって留年を免れたという。では実際に学生たちはどのように行動し、それは可能な限りの改善と不公平性の排除ができていたのか、これは今後、データを精査することで明らかになるだろう。マーケットデザインで大切なことは、導入して終わりではなく、現実とのギャップをさらに埋めていく作業(実証)がまだ残っているということである。
